Tomonaga–Luttinger Liquid in the Edge Channels of a Quantum Spin Hall Insulator
Result of the Month
The topological protection of the 1D metallic edge channels in QSH insulators against elastic single-particle backscattering is guaranteed by time-reversal symmetry. It leads to the QSH effect with its quantized conductance 2e2/h and dissipationless transport. Together with the property of the edge states being helical, i.e. the spin of electronic excitations is bound to their direction of motion, renders QSH insulators promising candidate materials for future device applications in spintronics.
The reported quantized conductance 2e2/h which can mostly be understood within topological band theory of non-interacting electrons, however, shows deviations from a sharply quantized value 2e2/h at very low temperatures in InAs/GaSb transport measurements. These observations have been attributed to the relevance of electronic interactions [2]. The latter stem from Coulomb interactions that are present in any real QSH insulator and thus can alter the 1D edge state conduction.
To capture the relevant physics, the oversimplified topological band theory must be complemented by the theory of (helical) Tomonaga-Luttinger liquids (TLL), which describes the boundary states as interacting 1D-spin polarized electrons [3]. However, a direct spectroscopic identification of this correlated many-body state in the edge states of a QSH insulator has not been reported so far, for lack of suitable material systems.
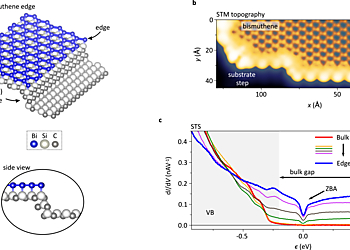
Here, bismuthene, i.e., a 2D monolayer of Bi atoms epitaxially grown on a semiconducting SiC(0001) substrate, turns out to be a particularly well-suited system for such studies. The strong atomic spin-orbit coupling in the Bi atoms conspires with their honeycomb arrangement and covalent coupling to the substrate to drive the system into a non-trivial topology [1]. STM/STS measurements have indicated the existence of conducting edge channels which due to the large bulk band gap of 0.8 eV display a strong localization at the edge, and which exponentially decay into the insulating 2D bulk within the extremely small value of 4.1 Å.
It is well-established that electronic interactions play a crucial role in such near-to-perfect 1D metallic systems. Under these circumstances the Fermi liquid description breaks down and the physics is dominated by collective bosonic excitations that can be described by TLL theory [4]. One common characteristic inherent to all TLLs is a power-law behaviour of their single-particle spectrum, r ~ |e|a for |e| >> kBT [5], directly accessible by STS [6]. In fact, the energy dependence emerges from an even more fundamental property of TLLs, namely the universal scaling in both energy and temperature according to which the power-law in energy is accompanied by a power-law of the zero-energy spectral weight as a function of temperature with the identical power-law exponent [7].
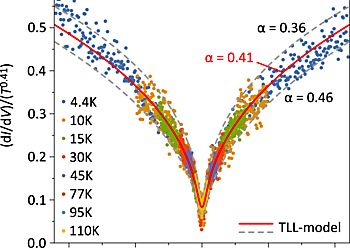
The property of universal scaling upon variation of energy and temperature can be visualized by a simultaneous plot of the tunneling spectra. In Fig. 2 the experimental dI/dV data are normalized to T0.41 and plotted versus e/kBT. Unambiguously all spectra collapse onto a single universal curve (red curve) as predicted for a TLL [7]. Our observations provide critical proof to render bismuthene the first QSH insulator for which a TLL behavior has been established and studied on the atomic scale.
References:
[1] F. Reis, G. Li, L. Dudy, M. Bauernfeind, S. Glass, W. Hanke, R. Thomale, J. Schäfer, and R. Claessen, „Bismuthene on a SiC substrate: A candidate for a high temperature quantum spin Hall material“, Science 357, 287 - 290 (2017).
[2] T. Li, P. Wang, H. Fu, L. Du, K. A. Schreiber, X. Mu, X. Liu, G. Sullivan, G. A. Csáthy, X. Lin, and R.-R. Du, „Observation of a Helical Luttinger Liquid in InAs/GaSb Quantum Spin Hall Edges“, Phys. Rev. Lett. 115, 136804 (2015).
[3] C. Wu, B. A. Bernevig, and S.-C. Zhang, „Helical Liquid and the Edge of Quantum Spin Hall Systems“, Phys. Rev. Lett. 96, 106401 (2006).
[4] F. D. M. Haldane, „‘Luttinger liquid theory' of one-dimensional quantum fluids. I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas“, Journal of Physics C: Solid State Physics 14, 2585 - 2609 (1981).
[5] B. Braunecker, C. Bena, and P. Simon, „Spectral properties of Luttinger liquids: A comparative analysis of regular, helical, and spiral Luttinger liquids“, Phys. Rev. B 85, 035136 (2012).
[6] S. Eggert, „Scanning Tunneling Microscopy of a Luttinger Liquid“, Phys. Rev. Lett. 84, 4413 - 4416 (2000).
[7] C. Blumenstein, J. Schäfer, S. Mietke, S. Meyer, A. Dollinger, M. Lochner, X. Y. Cui, L. Patthey, R. Matzdorf, and R. Claessen, „Atomically controlled quantum chains hosting a Tomonaga-Luttinger liquid“, Nat. Phys. 7, 776 - 780 (2011).
Authors:
R. Stühler, F. Reis, T. Müller, T. Helbig, T. Schwemmer, R. Thomale, J. Schäfer, R. Claessen
Institutes:
Physikalisches Institut Universität Würzburg and Würzburg-Dresden Cluster of Excellence ct.qmat
Institut für Theoretische Physik und Astrophysik Universität Würzburg
Name and email of corresponding author:
Raul Stühler, Universität Würzburg
raul.stuehler@physik.uni-wuerzburg.de